实验三 二叉树的基本操作（建立）及遍历

实验目的 1．学会实现二叉树结点结构和对二叉树的基本操作。 2．通过对二叉树遍历操作的实现，理解二叉树各种操作，学会利用递归方法编写对二叉树等类似递归数据结构进行处理的算法。 实验要求 1．认真阅读和掌握和本实验相关的教材内容。 2．编写完整程序完成下面的实验内容并上机运行。 实验内容 1．编写程序输入二叉树的结点个数和结点值，构造下图所示的二叉树。 2．编写程序，采用中序遍历的递归和非递归算法对此二叉树进行遍历。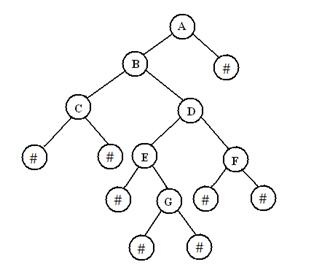 提示 从键盘接受输入（先序），以二叉链表作为存储结构，建立二叉树（以先序来建立）， [测试数据] 如输入：ABC＃＃DE＃G＃＃F＃＃＃（其中＃表示空格字符） 则输出结果为 先序：ABCDEGF 中序：CBEGDFA 后序：CGEFDBA 层序：ABCDEFG

下面是代码，供参考：

#include 
     
      #include 
      
       #define MAX 20#define NULL 0typedef char TElemType;typedef int  Status;typedef struct BiTNode{    TElemType data;    struct BiTNode *lchild,*rchild;} BiTNode,*BiTree;Status CreateBiTree(BiTree *T) ///BiTNode T{    char ch;    ch=getchar();    if(ch=='#')(*T)=NULL;///#代表空指针    else    {        (*T)=(BiTree)malloc(sizeof(BiTNode));        (*T)->data=ch;///生成根结点        CreateBiTree(&(*T)->lchild);///构造左子树        CreateBiTree(&(*T)->rchild);///构造右子树    }    return 1;}///先序遍历输出void PreOrder(BiTree T){    if(T)    {        printf("%2c",T->data);///T->data==(*T).data        PreOrder(T->lchild);///先序遍历左子树        PreOrder(T->rchild);///先序遍历右子树    }}///中序遍历输出void InOrder(BiTree T){    if(T)    {        InOrder(T->rchild);///中序遍历右子树        printf("%2c",T->data);        InOrder(T->lchild);///中序遍历左子树    }}///后序遍历输出void Postorder(BiTree T){    if(T)    {        Postorder(T->lchild);///后序遍历左子树        Postorder(T->rchild);///后序遍历右子树        printf("%2c",T->data);///访问根结点    }}///层次遍历二叉树T，从第一层开始，每层从左到右void LevleOrder(BiTree T){    BiTree Queue[MAX],b;    ///用一维数组表示队列，front和rear分别表示队首和队尾指针    int front,rear;    front=rear=0;    if(T) ///若树非空    {        Queue[rear++]=T;///根结点入队列        while(front!=rear) ///当队列非空        {            b=Queue[front++];///队首元素出队列，并访问这个结点            printf("%2c",b->data);            if(b->lchild!=NULL)            {                Queue[rear++]=b->lchild;                ///左子树非空，则入队列            }            if(b->rchild!=NULL)            {                Queue[rear++]=b->rchild;                ///右子树非空，则入队列            }        }    }}///求二叉树的深度int depth(BiTree T){    int dep1,dep2;    if(T==NULL)  return 0;    else    {        dep1=depth(T->lchild);        dep2=depth(T->rchild);        return dep1>dep2?dep1+1:dep2+1;    }}int main(){    BiTree T=NULL;///（开始定义的是*T）此时T为地址    printf("\n(Create a Binary Tree )建立一棵二叉树T:\n");    CreateBiTree(&T);///建立一棵二叉树    printf("\nThe preorder(先序序列为)is:\n");    PreOrder(T);    printf("\nThe inorder(中序序列为)is:\n");    InOrder(T);    printf("\nThe Postorder(后序序列为)is:\n");    Postorder(T);    printf("\nThe levle order(层次序列为)is:\n");    LevleOrder(T);    printf("\nThe depth(深度)is:%d\n",depth(T));    getchar();    return 0;}